- Research Article
- Open access
- Published:
Accelerating Seismic Computations Using Customized Number Representations on FPGAs
EURASIP Journal on Embedded Systems volume 2009, Article number: 382983 (2008)
Abstract
The oil and gas industry has an increasingly large demand for high-performance computation over huge volume of data. Compared to common processors, field-programable gate arrays (FPGAs) can boost the computation performance with a streaming computation architecture and the support for application-specific number representation. With hardware support for reconfigurable number format and bit width, reduced precision can greatly decrease the area cost and I/O bandwidth of the design, thus multiplying the performance with concurrent processing cores on an FPGA. In this paper, we present a tool to determine the minimum number precision that still provides acceptable accuracy for seismic applications. By using the minimized number format, we implement core algorithms in seismic applications (the FK step in forward continued-based migration and 3D convolution in reverse time migration) on FPGA and show speedups ranging from 5 to 7 by including the transfer time to and from the processors. Provided sufficient bandwidth between CPU and FPGA, we show that a further increase to 48X speedup is possible.
1. Introduction
Seismic imaging applications in oil and gas industry involves terabytes of data collected from fields. For each data sample, the imaging algorithm usually tries to improve the image quality by performing more costly computations. Thus, there is an increasingly large demand for high-performance computation over huge volume of data. Among all the different kinds of imaging algorithms, downward continued-based migration [1] is the most prevalent high-end imaging technique today and reverse time migration appears to be one of the dominant imaging techniques of the future.
Compared to conventional microprocessors, FPGAs apply a different streaming computation architecture. Computations we want to perform are mapped into circuit units on the FPGA board. Previous work has already achieved 20X acceleration for prestack Kirchhoff time migration [2] and 40X acceleration for subsurface offset gathers [3].
Besides the capability of performing computations in a parallel way, FPGAs also support application-specific number representations. Since all the processing units and connections on the FPGA are reconfigurable, we can use different number representations, such as fixed-point, floating-point, logarithmic number system (LNS), residue number system (RNS), and so forth, with different bit-width settings. Different number representations lead to different complexity of the arithmetic units, thus different costs and performances of the resulting circuit design [4]. Switching to a number representation that fits a given application better can sometimes greatly improve the performance or reduce the cost.
A simple case of switching number representations is to trade off precision of the number representation with the speed of the computation. For example, by reducing the precision from 32-bit floating-point to 16-bit fixed-point, the number of arithmetic units that fit into the same area can be increased by scores of times. The performance of the application is also improved significantly. Meanwhile, we also need to watch for the possible degradation of accuracy in the computation results. We need to check whether the accelerated computation using reduced precision is still generating meaningful results.
To solve the above problem in the seismic application domain, we develop a tool that performs an automated precision exploration of different number formats, and figures out the minimum precision that can still generate good enough seismic results. By using the minimized number format, we implement core algorithms in seismic applications (complex exponential step in forward continued based migration and 3D convolution in reverse time migration) on FPGA and show speedups ranging from 5 to 7 by including the transfer time to and from the processors. Provided sufficient bandwidth between CPU and FPGA, we show that a further increase to 48X speedup is possible.
2. Background
2.1. Number Representation
As mentioned in Section 1, precision and range are key resources to be traded off against the performance of a computation. In this work, we look at two different types of number representation: fixed-point and floating-point.
Fixed-Point Numbers
The fixed-point number has two parts, the integer part and the fractional part. It is in a format as shown in Table 1.
When it uses a sign-magnitude format (the first bit defines the sign of the number), its value is given by  . It may also use a two-complement format to indicate the sign.
. It may also use a two-complement format to indicate the sign.
Floating-Point Numbers
According to IEEE-754 standard, floating-point numbers can be divided into three parts: the sign bit, the exponent, and the mantissa, shown as in Table 2.
Their values are given by  . The sign bit defines the sign of the number. The exponent part uses a biased format. Its value equals to the sum of the original value and the bias, which is defined as
. The sign bit defines the sign of the number. The exponent part uses a biased format. Its value equals to the sum of the original value and the bias, which is defined as  . The extreme values of the exponent (
. The extreme values of the exponent ( and
and  are used for special cases, such as values of zero and
are used for special cases, such as values of zero and  . The mantissa is an unsigned fractional number, with an implied "1" to the left of the radix point.
. The mantissa is an unsigned fractional number, with an implied "1" to the left of the radix point.
2.2. Hardware Compilation Tool
We use a stream compiler (ASC) [5] as our hardware compilation tool to develop a range of different solutions for seismic applications. ASC was developed following research at Stanford University and Bell Labs, and is now commercialized by Maxeler Technologies. ASC enables the use of FPGAs as highly parallel stream processors. ASC is a C-like programming environment for FPGAs. ASC code makes use of C++ syntax and ASC semantics which allow the user to program on the architecture level, the arithmetic level, and the gate level. ASC provides the productivity of high-level hardware design tools and the performance of low-level optimized hardware design. On the arithmetic level, PAM-Blox II provides an interface for custom arithmetic optimization. On the higher level, ASC provides types and operators to enable research on custom data representation and arithmetic. ASC hardware types are HWint, HWfix, and HWfloat. Utilizing the data-types, we build libraries such as a function evaluation library or develop special circuits to solve particular computational problems such as graph algorithms. Algorithm 1 shows a simple example of an ASC description for a stream architecture that doubles the input and adds "55."
Algorithm 1: A simple ASC example.
// ASC code starts here
STREAM_START;
// Hardware Variable Declarations
HWint in (IN);
HWint out (OUT);
HWint tmp (TMP);
STREAM_LOOP (16);
tmp = (in  )
)  55;
55;
out = tmp;
// ASC code ends here
STREAM_END;
The ASC code segment shows HWint variables and the familiar C syntax for equations and assignments. Compiling this program with "gcc" and running it creates a netlist which can be transformed into a configuration bitstream for an FPGA.
2.3. Precision Analysis
There exist a number of research projects that focus on precision analysis, most of which are static methods that operate on the computational flow of the design and uses techniques based on range and error propagation to perform the analysis.
Lee et al. [6] present a static precision analysis technique which uses affine arithmetic to derive an error model of the design and applies simulated annealing to find out minimum bit widths to satisfy the given error requirement. A similar approach is shown in a bit-width optimization tool called Prcis [7].
These techniques are able to perform an automated precision analysis of the design and provide optimized bit widths for the variables. However, they are not quite suitable for seismic imaging algorithms. The first reason is that seismic imaging algorithms usually involve numerous iterations, which can lead to overestimation of the error bounds and derive a meaningless error function. Secondly, the computation in the seismic algorithms does not have a clear error requirement. We can only judge the accuracy of the computation from the generated seismic image. Therefore, we choose to use a dynamic simulation method to explore different precisions, detailed in Sections 3.3 and 3.4.
2.4. Computation Bottlenecks in Seismic Applications
Downward-continued migration comes in various flavors including common azimuth migration [8], shot profile migration, source-receiver migration, plane-wave or delayed shot migration, and narrow azimuth migration. Depending on the flavor of the downward continuation algorithm, there are four potential computation bottlenecks.
-
(i)
In many cases, the dominant cost is the FFT step. The dimensionality of the FFT varies from 1D (tilted plane-wave migration [9]) to 4D (narrow azimuth migration [10]). The FFT cost is often dominant due to its
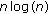 cost ratio,
cost ratio,  being the number of points in the transform, and the noncache friendly nature of multidimensional FFTs.
being the number of points in the transform, and the noncache friendly nature of multidimensional FFTs. -
(ii)
The FK step, which involves evaluating (or looking up) a square root function and performing complex exponential is a second potential bottleneck. The high operational count per sample can eat up significant cycles.
-
(iii)
The FX step, which involves a complex exponential, or sine/cosine multiplication, has a similar, but computationally less demanding, profile. Subsurface offset gathers for shot profile or plane-wave migration, particularly 3D subsurface offset gathers, can be an overwhelming cost. The large op-count per sample and the noncache friendly nature of the data usage pattern can be problematic.
-
(iv)
For finite difference-based schemes, a significant convolution cost can be involved.
The primary bottleneck of reverse time migration is applying the finite-different stencil. In addition to the large operation count (5 to 31 samples per cell) the access pattern has poor cache behavior for real size problems. Beyond applying the 3D stencil, the next most dominant cost is implementing damping boundary conditions. Methods such as perfectly matched layers (PMLs) can be costly [11]. Finally, if you want to use reverse time migration for velocity analysis, subsurface offset gathers need to be generated. The same cost profile that exists in downward continued-based migration exists for reverse time migration.
In this paper, we focus on two of the above computation bottlenecks: one is the FK step in forward continued-based migration, which includes a square root function and a complex exponential operation; the other one is the 3D convolution in reverse time migration. We perform automated precision exploration of these two computation cores, so as to figure out the minimum precision that can still generate accurate enough seismic images.
3. A Tool for Number Representation Exploration
FPGA-based implementations have the advantage over current software-based implementations of being able to use customizable number representations in their circuit designs. On a software platform, users are usually constrained to a few fixed number representations, such as 32/64-bit integers and single/double-precision floating-point, while the reconfigurable logic and connections on an FPGA enables the users to explore various kinds of number formats with arbitrary bit widths. Furthermore, users are also able to design the arithmetic operations for these customized number representations, thus can provide a highly customized solution for a given problem.
In general, to provide a customized number representation for an application, we need to determine the following three things.
-
(i)
Format of The Number Representation
There are existing FPGA applications using fixed-point, floating-point, and logarithmic number system (LNS) [12]. Each of the three number representations has its own advantages and disadvantages over the others. For instance, fixed-point has simple arithmetic implementations, while floating-point and LNS provide a wide representation range. It is usually not possible to figure out the optimal format directly. Exploration is needed to guide the selection.
-
(ii)
Bit Widths of Variables
This problem is generally referred to as bit width or word-length optimization [6, 13]. We can further divide this into two different parts: range analysis considers the problem of ensuring that a given variable inside a design has a sufficient number of bits to represent the range of the numbers, while in precision analysis, the objective is to find the minimum number of precision bits for the variables in the design such that the output precision requirements of the design are met.
-
(iii)
Design of The Arithmetic Units
The arithmetic operations of each number system are quite different. For instance, in LNS, multiplication, division, and exponential operations become as simple as addition or shift operations, while addition and subtraction become nonlinear functions to approximate. The arithmetic operations of regular data formats, such as fixed-point and floating-point, also have different algorithms with different design characteristics. On the other hand, evaluation of elementary functions plays a large part in seismic applications (trigonometric and exponential functions). Different evaluation methods and configurations can be used to produce evaluation units with different accuracies and performance.
This section presents our tool that tries to figure out the above three design options by exploring all the possible number representations. The tool is partly based on our previous work on bit-width optimization [6] and comparison between different number representations [14, 15].
Figure 1 shows our basic work flow to explore different number representations for a seismic application. We manually partition the Fortran program into two parts: one part runs on CPUs and we try to accelerate the other part (target code) on FPGAs. The partition is based on two metrics: (1) the target code shall consume a large portion of processing time in the entire program, otherwise the acceleration does not bring enough performance improvement to the entire application; (2) the target code shall be suitable for a streaming implementation on FPGA, thus highly probable to accelerate. After partition, the first step is to profile the target code to acquire information about the range of values and their distribution that each variable can take. In the second step, based on the range information, we map theFortrancode into a hardware design described in ASC format, which includes implementation of arithmetic operations and function evaluation. In the third step, the ASC description is translated into bit-accurate simulation code, and merged into the original Fortran program to provide a value simulator for the original application. Using this value simulator, explorations can be performed with configurable settings such as different number representations, different bit widths, and different arithmetic algorithms. Based on the exploration results, we can determine the optimal number format for this application with regards to certain metrics such as circuit area and performance.
3.1. Range Profiling
In the profiling stage, the major objective is to collect range and distribution information for the variables. The idea of our approach is to instrument every target variable in the code, adding function calls to initialize data structures for recording range information and to modify the recorded information when the variable value changes.
For the range information of the target variables (variables to map into the circuit design), we keep a record of four specific points on the axis, shown in Figure 2. The points  and
and  represent the values far away from zero, that is, the maximum absolute values that need to be represented. Based on their values, the integer bit width of fixed-point numbers can be determined. Points
represent the values far away from zero, that is, the maximum absolute values that need to be represented. Based on their values, the integer bit width of fixed-point numbers can be determined. Points  and
and  represent the values close to zero, that is, the minimum absolute values that need to be represented. Using both the minimum and maximum values, the exponent bit width of floating-point numbers can be determined.
represent the values close to zero, that is, the minimum absolute values that need to be represented. Using both the minimum and maximum values, the exponent bit width of floating-point numbers can be determined.
For the distribution information of each target variable, we keep a number of buckets to store the frequency of values at different intervals. Figure 3 shows the distribution information recorded for the real part of variable "wfld" (a complex variable). In each interval, the frequency of positive and negative values is recorded separately. The results show that, for the real part of variable "wfld," in each interval, the frequencies of positive and negative values are quite similar, and the major distribution of the values falls into the range  to
to  .
.
The distribution information provides a rough metric for the users to make an initial guess about which number representations to use. If the values of the variables cover a wide range, floating-point and LNS number formats are usually more suitable. Otherwise, fixed-point numbers shall be enough to handle the range.
3.2. Circuit Design: Basic Arithmetic and Elementary Function Evaluation
After profiling range information for the variables in the target code, the second step is to map the code into a circuit design described in ASC. As a high-level FPGA programming language, ASC provides hardware data types, such as HWint, HWfix, and HWfloat. Users can specify the bit-width values for hardware variables, and ASC automatically generates corresponding arithmetic units for the specified bit widths. It also provides configurable options to specify different optimization modes, such as AREA, LATENCY, and THROUGHPUT. In the THROUGHPUT optimization mode, ASC automatically generates a fully pipelined circuit. These features make ASC an ideal hardware compilation tool to retarget a piece of software code onto the FPGA hardware platform.
With support for fixed-point and floating-point arithmetic operations, the target Fortran code can be transformed into ASC C++ code in a straightforward manner. We also have interfaces provided by ASC to modify the internal settings of these arithmetic units.
Besides basic arithmetic operations, evaluation of elementary functions takes a large part in seismic applications. For instance, in the first piece of target code we try to accelerate, the FK step, a large portion of the computation is to evaluate the square root and sine/cosine functions. To map these functions into efficient units on the FPGA board, we use a table-based uniform polynomial approximation approach, based on Dong-U Lee's work on optimizing hardware function evaluation [16]. The evaluation of the two functions can be divided into three different phases [17].
-
(i)
Range reduction: reduce the range of the input variable
 into a small interval that is convenient for the evaluation procedure. The reduction can be multiplicative (e.g.,
into a small interval that is convenient for the evaluation procedure. The reduction can be multiplicative (e.g., 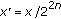 for square root function) or additive (e.g.,
for square root function) or additive (e.g., 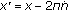 for sine/cosine functions).
for sine/cosine functions). -
(ii)
Function evaluation: approximate the value of the function using a polynomial within the small interval.
-
(iii)
Range reconstructions: map the value of the function in the small interval back into the full range of the input variable
 .
.
To keep the whole unit small and efficient, we use degree-one polynomial so that only one multiplication and one addition are needed to produce the evaluation result. Meanwhile, to preserve the approximation error at a small scale, the reduced evaluation range is divided into uniform segments. Each segment is approximated with a degree-one polynomial, using the minimax algorithm. In the FK step, the square root function is approximated with 384 segments in the range of [0.25, 1] with a maximum approximation error of  , while the sine and cosine functions are approximated with 512 segments in the range of [0, 2] with a maximum approximation error of
, while the sine and cosine functions are approximated with 512 segments in the range of [0, 2] with a maximum approximation error of  .
.
3.3. Bit-Accurate Value Simulator
As discussed in Section 3.1, based on the range information, we are able to determine the integer bit width of fixed-point, and partly determine the exponent bit width of floating-point numbers (as exponent bit width does not only relate to the range but also to the accuracy). The remaining bit widths, such as the fractional bit width of fixed-point, and the mantissa bit width of floating-point numbers, are predominantly related to the precision of the calculation. In order to find out the minimum acceptable values for these precision bit widths, we need a mechanism to determine whether a given set of bit-width values produce satisfactory results for the application.
In our previous work on function evaluation or other arithmetic designs, we set a requirement of the absolute error of the whole calculation, and use a conservative error model to determine whether the current bit-width values meet the requirement or not [6]. However, a specified requirement for absolute error does not work for seismic processing. To find out whether the current configuration of precision bit width is accurate enough, we need to run the whole program to produce the seismic image, and find out whether the image contains the correct pattern information. Thus, to enable exploration of different bit-width values, a value simulator for different number representations is needed to provide bit-accurate simulation results for the hardware designs.
With the requirement to produce bit-accurate results as the corresponding hardware design, the simulator also needs to be efficiently implemented, as we need to run the whole application (which takes days using the whole input dataset) to produce the image.
In our approach, the simulator works with ASC format C++ code. It reimplements the ASC hardware data types, such as HWfix and HWfloat, and overloads their arithmetic operators with the corresponding simulation code. For HWfix variables, the value is stored in a 64-bit signed integer, while another integer is used to record the fractional point. The basic arithmetic operations are mapped into shifts and arithmetic operations of the 64-bit integers. For HWfloat variables, the value is stored in a 80-bit extended-precision floating-point number, with two other integers used to record the exponent and mantissa bit width. To keep the simulation simple and fast, the arithmetic operations are processed using floating-point values. However, to keep the result bit accurate, during each assignment, by performing corresponding bit operations, we decompose the floating-point value into mantissa and exponent, truncate according to the exponent and mantissa bit widths, and combine them back into the floating-point value.
3.4. Accuracy Evaluation of Generated Seismic Images
As mentioned above, the accuracy of a generated seismic image depends on the pattern contained inside, which estimates the geophysical status of the investigated area. To judge whether the image is accurate enough, we compare it to a "target" image, which is processed using single-precision floating-point and assumed to contain the correct pattern.
To perform this pattern comparison automatically, we use techniques based on prediction error filters (PEFs) [18] to highlight differences between two images. The basic work flow of comparing image  to image
to image  (assume image
(assume image  is the "target" image) is as follows.
is the "target" image) is as follows.
-
(i)
Divide image
 into overlapping small regions of
into overlapping small regions of 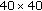 pixels, and estimate PEFs for these small regions.
pixels, and estimate PEFs for these small regions. -
(ii)
Apply these PEFs to both image
 and image
and image 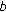 to get the results
to get the results  and
and  .
. -
(iii)
Apply algebraic combinations of the images
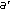 and
and 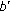 to acquire a value indicating the image differences.
to acquire a value indicating the image differences.
By the end of the above work flow, we achieve a single value which describes the difference from the generated image to the "target image." For convenience of discussion afterwards, we call this value as "difference indicator" (DI).
Figure 4 shows a set of different seismic images calculated from the same dataset, and their DI values compared to the image with correct pattern. The image showing correct pattern is calculated using single-precision floating-point, while the other images are calculated using fixed-point designs with different bit-width settings. All these images are results of the bit-accurate value simulator mentioned above.
If the generated image contains no information at all (as shown in Figure 4(a)), the comparison does not return a finite value. This is mostly because a very low precision is used for the calculation. The information is lost during numerous iterations and the result only contains zeros or infinities. If the comparison result is in the range of  to
to  (Figures 4(b) and 4(c)), the image contains random pattern which is far different from the correct one. With a comparison result in the range of
(Figures 4(b) and 4(c)), the image contains random pattern which is far different from the correct one. With a comparison result in the range of  (Figure 4(d)), the image contains similar pattern to the correct one, but information in some parts is lost. With a comparison result in the range of
(Figure 4(d)), the image contains similar pattern to the correct one, but information in some parts is lost. With a comparison result in the range of  or smaller, the generated image contains almost the same pattern as the correct one.
or smaller, the generated image contains almost the same pattern as the correct one.
Note that the DI value is calculated from algebraic operations on the two images you compare with. The magnitude of DI value is only a relative indication of the difference between the two images. The actual usage of the DI value is to figure out the boundary between the images that contains mostly noises and the images that provide useful patterns of the earth model. From the samples shown in Figure 7, in this specific case, the DI value of  is a good guidance value for acceptable accuracy of the design. From the bit-width exploration results shown in Section 4, we can see that the DI value of
is a good guidance value for acceptable accuracy of the design. From the bit-width exploration results shown in Section 4, we can see that the DI value of  also happens to be a precision threshold, where the image turns from noise into accurate pattern with the increase of bit width.
also happens to be a precision threshold, where the image turns from noise into accurate pattern with the increase of bit width.
3.5. Number Representation Exploration
Based on all the above modules, we can now perform exploration of different number representations for the FPGA implementation of a specific piece of Fortran code.
The current tools support two different number representations, fixed-point, and floating-point numbers (the value simulator for LNS is still in progress). For all the different number formats, the users can also specify arbitrary bit widths for each different variable.
There are usually a large number of different variables involved in one circuit design. In our previous work, we usually apply heuristic algorithms, such as ASA [19], to find out a close-to-optimal set of bit-width values for different variables. The heuristic algorithms may require millions of test runs to check whether a specific set of values meet the constraints or not. This is acceptable when the test run is only a simple error function and can be processed in nanoseconds. In our seismic processing application, depending on the problem size, it takes half an hour to several days to run one test set and achieve the result image. Thus, heuristic algorithms become impractical.
A simple and straightforward method to solve the problem is to use uniform bit width over all the different variables, and either iterate over a set of possible values or use a binary search algorithm to jump to an appropriate bit-width value. Based on the range information and the internal behavior of the program, we can also try to divide the variables in the target Fortran code into several different groups, and assign a different uniform bit width for each different group. For instance, in the FK step, there is a clear boundary that the first half performs square, square root, and division operations to calculate an integer value, and the second half uses the integer value as a table index, and performs sine, cosine, and complex multiplications to get the final result. Thus, in the hardware circuit design, we divide the variables into two groups based on which half it belongs to. Furthermore, in the second half of the function, some of the variables are trigonometric values in the range of  , while the other variables represent the seismic image data and scale up to
, while the other variables represent the seismic image data and scale up to  . Thus, they can be further divided into two parts and assigned bit widths separately.
. Thus, they can be further divided into two parts and assigned bit widths separately.
4. Case Study I: The FK Step in Downward Continued-Based Migration
4.1. Brief Introduction
The code shown in Algorithm 2 is the computationally intensive portion of the FK step in a downward continued-based migration. The governing equation for the FK step is the double square root equation (DSR) [20]. The DSR equation describes how to downward continue a wave-field  one depth
one depth  step. The equation is valid for a constant velocity medium
step. The equation is valid for a constant velocity medium  and is based on the wave number of the source
and is based on the wave number of the source  and receiver
and receiver  . The DSR equation can be written as (1), where
. The DSR equation can be written as (1), where  is the frequency. The code takes the approach of building a priori a relatively small table of the possible values of
is the frequency. The code takes the approach of building a priori a relatively small table of the possible values of  . The code then performs a table lookup that converts a given
. The code then performs a table lookup that converts a given  value to an approximate value of the square root.
value to an approximate value of the square root.
Algorithm 2: The code for the major computations of the FK step.
! generation of table step%ctable
do i = 1, size (step%ctable)
 ∗ step%dstep ∗ dsr%phase (i)
∗ step%dstep ∗ dsr%phase (i)
step%ctable (i) = dsr%amp (i) ∗ cmplx (cos ( ), sin (
), sin ( ))
))
end do
! the core part of function wei_wem
do i4 = 1, size (wfld, 4)
do i3 = 1, size (wfld, 3)
do i2 = 1, size (wfld, 2)
do i1 = 1, size (wfld, 1)
 = sqrt (step%
= sqrt (step% (i1, i3) ∗ ∗ 2 + step%
(i1, i3) ∗ ∗ 2 + step% (i2, i4)∗ ∗ 2)
(i2, i4)∗ ∗ 2)
itable = max (1, min (int (1 + k / ko /dsr%d), dsr%n))
wfld (i1, i2, i3, i4, i5) = wfld (i1, i2, i3, i4, i5) ∗ step%ctable (itable)
end do
end do
end do
end do
In practical applications, "wfld" contains millions of data items. The computation pattern of this function makes it an ideal target to map to a streaming hardware circuit on an FPGA.
4.2. Circuit Design
The mapping from the software code to a hardware circuit design is straightforward for most parts. Figure 5 shows the general structure of the circuit design. Compared with the software Fortran code shown in Algorithm 2, one big difference is the handling of the sine and cosine functions. In the software code, the trigonometric functions are calculated outside the five-level loop, and stored as a lookup table. In the hardware design, to take advantage of the parallel calculation capability provided by the numerous logic units on the FPGA, the calculation of the sine/cosine functions is merged into the processing core of the inner loop. Three function evaluation units are included in this design to produce values for the square root, cosine and sine functions separately. As mentioned in Section 3.2, all three functions are evaluated using degree-one polynomial approximation with 386 or 512 uniform segments:

The other task in the hardware circuit design is to map the calculation into arithmetic operations of certain number representations. Table 3 shows the value range of some typical variables in the FK step. Some of the variables (in the part of square root and sine/cosine function evaluations) have a small range within [0, 1], while other values (especially "wfld" data) have a wide range from  to
to  . If we use floating-point or LNS number representations, their wide representation ranges are enough to handle these variables. However, if we use fixed-point number representations in the design, special handling is needed to achieve acceptable accuracy over wide ranges.
. If we use floating-point or LNS number representations, their wide representation ranges are enough to handle these variables. However, if we use fixed-point number representations in the design, special handling is needed to achieve acceptable accuracy over wide ranges.
The first issue to consider in fixed-point designs is the enlarged error caused by the division after the evaluation of the square root ( ). The values of
). The values of  ,
,  and
and  come from the software program as input values to the hardware circuit, and contain errors propagated from previous calculations or caused by the truncation/rounding into the specified bit width on hardware. Suppose the error in the square root result
come from the software program as input values to the hardware circuit, and contain errors propagated from previous calculations or caused by the truncation/rounding into the specified bit width on hardware. Suppose the error in the square root result  is
is  , and the error in variable
, and the error in variable  is
is  , assuming that the division unit itself does not bring extra error, the error in the division result is given by
, assuming that the division unit itself does not bring extra error, the error in the division result is given by  . According to the profiling results,
. According to the profiling results,  holds a dynamic range from
holds a dynamic range from  to
to  , and
, and  has a maximum value of
has a maximum value of  (variables step%
(variables step% and step%
and step% have similar ranges). In the worst case, the error from
have similar ranges). In the worst case, the error from  can be magnified by 70 times, and the error from
can be magnified by 70 times, and the error from  magnified by approximately 9000 times.
magnified by approximately 9000 times.
To solve the problem of enlarged errors, we perform shifts at the input side to keep the three values  ,
,  and
and  in a similar range. The variable
in a similar range. The variable  is shifted by the distance
is shifted by the distance  so that the value after shifting falls in the range of
so that the value after shifting falls in the range of  . The variables
. The variables  and
and  are shifted by another distance
are shifted by another distance  so that the larger value of the two also falls in the range of
so that the larger value of the two also falls in the range of  . The difference between
. The difference between  and
and  is recorded so that after the division, the result can be shifted back into the correct scale. In this way, the
is recorded so that after the division, the result can be shifted back into the correct scale. In this way, the  has a range of
has a range of  and
and  has a range of
has a range of  . Thus, the division only magnifies the errors by an order of 3 to 6. Meanwhile, as the three variables
. Thus, the division only magnifies the errors by an order of 3 to 6. Meanwhile, as the three variables  ,
,  and
and  are originally in single-precision floating-point representation in software, when we pass their values after shifts, a large part of the information stored in the mantissa part can be preserved. Thus, a better accuracy is achieved through the shifting mechanism for fixed-point designs.
are originally in single-precision floating-point representation in software, when we pass their values after shifts, a large part of the information stored in the mantissa part can be preserved. Thus, a better accuracy is achieved through the shifting mechanism for fixed-point designs.
Figure 6 shows experimental results about the accuracy of the table index calculation when using shifting compared to not using shifting, with different uniform bit widths. The possible range of the table index result is from 1 to 2001. As it is the index for tables of smooth sequential values, an error within five indices is generally acceptable. We use the table index results calculated with single-precision floating-point as the true values for error calculation. When the uniform bit width of the design changes from 10 to 20, designs using the shifting mechanism show a stable maximum error of 3, and an average error around 0.11. On the other hand, the maximum error of designs without shifting vary from 2000 to 75, and the average errors vary from approximately 148 to 0.5. These results show that the shifting mechanism provides much better accuracy for the part of the table index calculation in fixed-point designs.
The other issue to consider is the representation of "wfld" data variables. As shown in Table 3, both the real and imaginary parts of "wfld" data have a wide range from  to
to  . Generally, fixed-point numbers are not suitable to represent such wide ranges. However, in this seismic application, the "wfld" data is used to store the processed image information. It is more important to preserve the pattern information shown in the data values rather than the data values themselves. Thus, by omitting the small values and using the limited bit width to store the information contained in large values, fixed-point representations still have a big chance to achieve accurate image in the final step. In our design, for convenience of bit-width exploration, we scale down all the "wfld" data values by a ratio of
. Generally, fixed-point numbers are not suitable to represent such wide ranges. However, in this seismic application, the "wfld" data is used to store the processed image information. It is more important to preserve the pattern information shown in the data values rather than the data values themselves. Thus, by omitting the small values and using the limited bit width to store the information contained in large values, fixed-point representations still have a big chance to achieve accurate image in the final step. In our design, for convenience of bit-width exploration, we scale down all the "wfld" data values by a ratio of  so that they fall into the range of [0,1).
so that they fall into the range of [0,1).
4.3. Bit-Width Exploration Results
The original software Fortran code of the FK step performs the whole computation using single-precision floating-point. We firstly replace the original Fortran code of the FK step with a piece of C++ code using double-precision floating-point to generate a full-precision image to compare with. After that, to investigate the effect of different number representations for variables in the FK step on the accuracy of the whole application, we replace the code of the FK step with our simulation code that can be configured with different number representations and different bit widths and generate results for different settings. The approach for accuracy evaluation, introduced in Section 3.4, is used to provide DI values that indicate the differences in the patterns of the resulted seismic images from the pattern in full-precision image.
4.3.1. Fixed-Point Designs
In the first step, we apply uniform bit width over all the variables in the design. We change the uniform bit width from 10 to 20. With of uniform bit width of 16, the design provides a DI value around 100, which means that the image contains a pattern almost the same to the correct one.
In the second step, as mentioned in Section 3.5, according to their characteristics in range and operational behavior, we can divide the variables in the design into different groups and apply a uniform bit width in each group. In the hardware design for the FK step, the variables are divided into three groups: SQRT, the part from the beginning to the table index calculation, which includes an evaluation of the square root; SINE, the part from the end of SQRT to the evaluation of the sine and cosine functions; WFLD, the part that multiplies the complex values of "wfld" data with a complex value consisting of the sine and cosine values (for phase modification), and a real value (for amplitude modification). To perform the accuracy investigation, we keep two of the bit-width values constant, and change the other one gradually to see its effect on the accuracy of the entire application.
Figure 7(a) shows the DI values of the generated images when we change the bit width of the SQRT part from 6 to 20. The bit widths of the SINE and WFLD parts are set to 20 and 30, respectively. Large bit widths are used for the other two parts so that they do not contribute much to the errors and the effect of variables bit width in SQRT can be extracted out. The case of SQRT bit widths shows a clear precision threshold at the bit-width value of 10. When the SQRT bit width increases from 8 bits to 10 bits, the DI value falls down from the scale of  to the scale of
to the scale of  . The significant improvement in accuracy is also demonstrated in the generated seismic images. The image on the left of Figure 7(a) is generated with 8-bit design. Compared to the "true" image calculated with single-precision floating-point, the lower part of the image is mainly noise signals, while the lower part starts to show a similar pattern as the correct ones. The difference between the qualities of the lower and upper parts is because of the imaging algorithm, which calculates the image from summation of a number of points at the corresponding depth. In acoustic models, there are generally more sample points when we go deeper into the earth. Therefore, using the same precision, the lower part shows a better quality than the upper part. The image on the right of Figure 7(a) is generated with 10-bit design, and already contains almost the same pattern as the "true" image.
. The significant improvement in accuracy is also demonstrated in the generated seismic images. The image on the left of Figure 7(a) is generated with 8-bit design. Compared to the "true" image calculated with single-precision floating-point, the lower part of the image is mainly noise signals, while the lower part starts to show a similar pattern as the correct ones. The difference between the qualities of the lower and upper parts is because of the imaging algorithm, which calculates the image from summation of a number of points at the corresponding depth. In acoustic models, there are generally more sample points when we go deeper into the earth. Therefore, using the same precision, the lower part shows a better quality than the upper part. The image on the right of Figure 7(a) is generated with 10-bit design, and already contains almost the same pattern as the "true" image.
In a similar way, we perform the exploration for the other two parts, and acquire the precision threshold 10, 12, and 16 for the SQRT, SINE, and WFLD parts, respectively. However, as the above results are acquired with two out of the three bit widths set to very large values, the practical solution shall be lightly larger than these values. Meanwhile, constrained by the current I/O bandwidth of 64 bits per second, the sum of the bit widths for SQRT and WFLD parts shall be less than 30. We perform further experiments for bit-width values around the initial guess point, and find out that bit widths of 12, 16, and 16 for the three parts provide a DI value of 131.5 and also meet the bandwidth requirement.
4.3.2. Floating-Point Designs
In floating-point design of the FK step, we perform an exploration of different exponent and mantissa bit widths. Similar to fixed-point designs, we use a uniform bit width for all the variables. When we investigate one of them, we keep the other one with a constant high value.
Figure 7(b) shows the case that we change the exponent bit width from 3 to 10, while we keep the mantissa bit width as 24. There is again a clear cut at the bit width of 6. When the exponent bit width is smaller than 6, the DI value of the generated image is at the level of  . When the exponent bit width increases to 6, the DI value decreases to around 1.
. When the exponent bit width increases to 6, the DI value decreases to around 1.
With a similar exploration of the mantissa bit width, we figure out that exponent bit width of 6 and mantissa bit width of 16 provide the minimum bit widths needed to achieve a DI value around  . Experiment confirms that this combination produces image with a DI value of 43.96.
. Experiment confirms that this combination produces image with a DI value of 43.96.
4.4. Hardware Acceleration Results
The hardware acceleration tool used in this project is the FPGA computing platform MAX-1, provided by Maxeler Technologies [21]. It contains a high-performance Xilinx Virtex IV FX100 FPGA, which consists of 42176 slices, 376 BRAMs, and 192 embedded multipliers. Meanwhile, it provides a high-bandwidth interface of PCI Express X8 (2 G bytes per second) to the software side residing in CPUs.
Based on the exploration results of different number representations, the fixed-point design with bit widths of 12, 16, and 16 for three different parts is selected in our hardware implementation. The design produces images containing the same pattern as the double-precision floating-point implementation, and has the smallest bit-width values, that is, the lowest resource cost among all the different number representations.
Table 4 shows the speedups we can achieve on FPGA compared to software solutions running on Intel Xeon CPU of 1.86 GHz. We experiment with two different sizes of datasets. For each of the datasets, we record the processing time for 10 000 times and calculate the average as the result. Speedups of 6.3 and 6.9 times are achieved for the two different datasets, respectively.
Table 5 shows the resource cost to implement the FK step on the FPGA card. It utilizes 28% of the logic units, 15% of the BRAMs (memory units) and 10% of the arithmetic units. Considering that a large part (around 20%) of the used logic units are circuits handling PCI-Express I/O, there is still much potential to put more processing cores onto the FPGA card and to gain even higher speedups.
5. Case Study Ii: 3d Convolution in Reverse Time Migration
3D convolution is one of the major computation bottlenecks in reverse time migration algorithms. In this paper, we implemented a 6th-order acoustic modeling kernel to investigate the potential speedups on FPGAs. The 3D convolution uses a kernel with 19 elements. Once each line of the kernel has been processed, it is scaled by a constant factor.
One of the key challenges to implement 3D convolution is how to keep a fast access to all the data elements needed for a 19-point operations. As the data items are generally stored in one direction, when you want to access the data items in a 3D pattern, you need to either buffer a large amount of data items or access them in a very slow nonlinear pattern. In our FPGA design, we solve this problem by buffering the current block we process into the BRAM FIFOs. ASC provides a convenient interface to automatically buffer the input values into BRAMs and the users can access them by specifying the cycle number that the value gets read in. Thus, we can easily index into the stream to obtain values already sent to the FPGA and perform the 3D operator.
Compared to the 3D convolution processed on CPUs, FPGA has two major advantages. One is the capability of performing computations in parallel. We exploit the parallelism of the FPGA to calculate one result per cycle. When ASC assigns the elements to BRAMs, it does so in such a way as to maximize the number of elements that can be obtained from the BRAM every cycle. This means that consecutive elements of the kernel must not in general be placed in the same BRAM. The other advantage is the support for application-specific number representations. By using fixed-point of 20 bits (the minimum bit-width setting that provides acceptable accuracy), we can reduce the area cost greatly thus put more processing units into the FPGA.
We test the convolution design on a data size of  . To compute the entire computation all at the same time (as is the case when a high-performance processor is used) requires a large local memory (in the case of the processor, a large cache). The FPGA has limited resources on-chip (376 BRAMs which can each hold 512 32 bit values). To solve this problem, we break the large dataset into cubes and process them separately. To utilize all of our input and output bandwidths, we assign 3 processing cores to the FPGA resulting in 3 inputs and 3 outputs per cycle at 125 MHz (constrained by the throughput of the PCI-Express bus). This gives us a theoretical maximum throughput of 375 M results a second.
. To compute the entire computation all at the same time (as is the case when a high-performance processor is used) requires a large local memory (in the case of the processor, a large cache). The FPGA has limited resources on-chip (376 BRAMs which can each hold 512 32 bit values). To solve this problem, we break the large dataset into cubes and process them separately. To utilize all of our input and output bandwidths, we assign 3 processing cores to the FPGA resulting in 3 inputs and 3 outputs per cycle at 125 MHz (constrained by the throughput of the PCI-Express bus). This gives us a theoretical maximum throughput of 375 M results a second.
The disadvantage of breaking the problem into smaller blocks is that the boundaries of each block are essentially wasted (although a minimal amount of reuse can occur) because they must be resent when the adjacent block is calculated. We do not consider this a problem since the blocks we use are at least  which means only a small proportion of the data is resent.
which means only a small proportion of the data is resent.
In software, the convolution executes in 11.2 seconds on average. The experiment was carried out using a dual-processor machine (each quad-core Intel Xeon 1.86 GHz) with 8 GB of memory.
In hardware, using the MAX-1 platform we perform the same computation in 2.2 seconds and obtain a 5 times speedup. The design uses 48 DSP blocks (30%), 369 (98%) RAMB16 blocks, and 30,571 (72%) of the slices on the Virtex IV chip. This means that there is room on the chip to substantially increase the kernel size. For a larger sized kernel (31 points), the speedup should be virtually linear, resulting in an 8 times speedup compared to the CPU implementation.
6. Further Potential Speedups
One of the major constraints for achieving higher speedups on FPGAs is the limited bandwidth between the FPGA card and the CPU. For the current PCI-Express interface provided by the MAX-1 platform, in each cycle, we can only read 8 bytes into the FPGA card and write back 8 bytes to the system.
An example is the implementation of the FK step, described in Section 4. As shown in Algorithm 2, in our current designs, we take  ,
,  and both the real and imaginary parts of
and both the real and imaginary parts of  as inputs to the circuit on FPGA, and take the modified real and imaginary parts of
as inputs to the circuit on FPGA, and take the modified real and imaginary parts of  as outputs. Therefore, although there is much space on the FPGA card to support multiple cores, the interface bandwidth can only support one single core and get a speedup of around 7 times.
as outputs. Therefore, although there is much space on the FPGA card to support multiple cores, the interface bandwidth can only support one single core and get a speedup of around 7 times.
However, in the specific case of FK step, there are further techniques we can utilize to gain some more speedups. From the codes in Algorithm 2, we can find out that  varies with all the four different loop indices, while
varies with all the four different loop indices, while  and
and  only vary with two of the four loop indices. To take advantage of this characteristic, we can divide the processing of the loop into two parts: in the first part, we use the bandwidth to read in the
only vary with two of the four loop indices. To take advantage of this characteristic, we can divide the processing of the loop into two parts: in the first part, we use the bandwidth to read in the  and
and  values, without doing any calculation; in the second part, we can devote the bandwidth to read in
values, without doing any calculation; in the second part, we can devote the bandwidth to read in  data only, and start the processing as well. In this pattern, suppose we are processing a
data only, and start the processing as well. In this pattern, suppose we are processing a  four-level loop, the bandwidth can support two cores processing concurrently while spending 1 out of 100 cycles to read in the
four-level loop, the bandwidth can support two cores processing concurrently while spending 1 out of 100 cycles to read in the  and
and  values in advance. In this way, we are able to achieve a speedup of
values in advance. In this way, we are able to achieve a speedup of  times. Furthermore, assume that there is an unlimited communication bandwidth, the cost of BRAMs (15%) becomes the major constraint. We can then put 6 concurrent cores on the FPGA card and achieve a speedup of
times. Furthermore, assume that there is an unlimited communication bandwidth, the cost of BRAMs (15%) becomes the major constraint. We can then put 6 concurrent cores on the FPGA card and achieve a speedup of  times.
times.
Another possibility is to put as much computation as possible onto the FPGA card, and reduce the communication cost between FPGA and CPU. If multiple portions of the algorithm are performed on the FPGA without returning to the CPU, the additional speedup can be considerable. For instance, as mentioned in Section 2, the major computation cost in downward continued-based migration lies in the multidimensional FFTs and the FK step. If the FFT and the FK step can reside simultaneously on the FPGA card, the communication cost between the FFT and the FK step can be eliminated completely. In the case of 3D convolution in reverse time migration, multiple time steps can be applied simultaneously.
7. Conclusions
This paper describes our work on accelerating seismic applications by using customized number representations on FPGAs. The focus is to improve the performance of the FK step in downward continued-based migration and the acoustic 3D convolution kernel in reverse time migration. To investigate the tradeoff between precision and speed, we develop a tool that performs an automated precision exploration of different number formats, and figures out the minimum precision that can still generate good enough seismic results. By using the minimized number format, we implement the FK step in forward continued-based migration and 3D convolution in reverse time migration on FPGA and show speedups ranging from 5 to 7 by including the transfer time to and from the processors. We also show that there are further potentials to accelerate these applications by above 10 or even 48 times.
References
Gazdag J, Sguazzero P: Migration of seismic data by phase shift plus interpolation. In Migration of Seismic Data. Edited by: Gardner GHF. Society of Exploration Geophysicists, Tulsa, Oklahoma; 1985.
He C, Lu M, Sun C: Accelerating seismic migration using FPGA-based coprocessor platform. Proceedings of the 12th Annual IEEE Symposium on Field-Programmable Custom Computing Machines (FCCM '04), April 2004, Napa, Calif, USA 207-216.
Pell O, Clapp RG: Accelerating subsurface offset gathers for 3D seismic applications using FPGAs. SEG Technical Program Expanded Abstracts 2007,26(1):2383-2387.
Deschamps J, Bioul G, Sutter G: Synthesis of Arithmetic Circuits: FPGA, ASIC and Embedded Systems. Wiley-Interscience, New York, NY, USA; 2006.
Mencer O: ASC: a stream compiler for computing with FPGAs. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 2006,25(9):1603-1617.
Lee D-U, Gaffar AA, Cheung RCC, Mencer O, Luk W, Constantinides GA: Accuracy-guaranteed bit-width optimization. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems 2006,25(10):1990-2000.
Chang ML, Hauck S: Precis: a usercentric word-length optimization tool. IEEE Design & Test of Computers 2005,22(4):349-361. 10.1109/MDT.2005.92
Biondi B, Palacharla G: 3-D prestack migration of common-azimuth data. Geophysics 1996,61(6):1822-1832. 10.1190/1.1444098
Shan G, Biondi B: Imaging steep salt flank with plane-wave migration in tilted coordinates. SEG Technical Program Expanded Abstracts 2006,25(1):2372-2376.
Biondi B: Narrow-azimuth migration of marine streamer data. SEG Technical Program Expanded Abstracts 2003,22(1):897-900.
Zhao L, Cangellaris AC: GT-PML: generalized theory of perfectly matched layers and its application to the reflectionless truncation of finite-difference time-domain grids. IEEE Transactions on Microwave Theory and Techniques 1996,44(12, part 2):2555-2563. 10.1109/22.554601
Matousek R, Tichy M, Pohl Z, Kadlec J, Softley C, Coleman N: Logarithmic number system and floating-point arithmetic on FPGA. Proceedings of the 12th International Conference on Field-Programmable Logic and Applications (FPL '02), August 2002, Madrid, Spain 627-636.
Constantinides GA, Cheung PYK, Luk W: Heuristic datapath allocation for multiple wordlength systems. Proceedings of the Conference on Design, Automation and Test in Europe (DATE '01), March 2001, Munich, Germany 791-796.
Fu H, Mencer O, Luk W: Comparing floating-point and logarithmic number representations for reconfigurable acceleration. Proceedings of the IEEE International Conference on Field Programmable Technology (FPT '06), December 2006, Bangkok, Thailand 337-340.
Fu H, Mencer O, Luk W: Optimizing logarithmic arithmetic on FPGAs. Proceedings of the 15th Annual IEEE Symposium on Field-Programme Custom Computing Machines (FCCM '07), April 2007, Napa, Calif, USA 163-172.
Lee D-U, Gaffar AA, Mencer O, Luk W: Optimizing hardware function evaluation. IEEE Transactions on Computers 2005,54(12):1520-1531. 10.1109/TC.2005.201
Muller J: Elementary Functions: Algorithms and Implementation. Birkhäuser, Secaucus, NJ, USA; 1997.
Claerbout J: Geophysical estimation by example: Environmental soundings image enhancement: Stanford Exploration Project. 1999, http://sepwww.stanford.edu/sep/prof/
Ingber L: Adaptive Simulated Annealing (ASA) 25.15. 2004, http://www.ingber.com/
Claerbout J: Basic Earth Imaging (BEI). 2000, http://sepwww.stanford.edu/sep/prof/
Maxeler Technologies http://www.maxeler.com
Acknowledgments
The support from the Center for Computational Earth and Environmental Science, Stanford Exploration Project, Computer Architecture Research Group at Imperial College London, and Maxeler Technologies is gratefully acknowledged. The authors also would like to thank Professor Martin Morf and Professor Michael Flynn for their support and advice.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Fu, H., Osborne, W., Clapp, R. et al. Accelerating Seismic Computations Using Customized Number Representations on FPGAs. J Embedded Systems 2009, 382983 (2008). https://doi.org/10.1155/2009/382983
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/382983
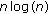 cost ratio,
cost ratio,  being the number of points in the transform, and the noncache friendly nature of multidimensional FFTs.
being the number of points in the transform, and the noncache friendly nature of multidimensional FFTs.


 is reserved for zero values. The other buckets with index
is reserved for zero values. The other buckets with index  store the values in the range
store the values in the range  .
. into a small interval that is convenient for the evaluation procedure. The reduction can be multiplicative (e.g.,
into a small interval that is convenient for the evaluation procedure. The reduction can be multiplicative (e.g., 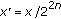 for square root function) or additive (e.g.,
for square root function) or additive (e.g., 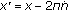 for sine/cosine functions).
for sine/cosine functions). .
. into overlapping small regions of
into overlapping small regions of 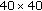 pixels, and estimate PEFs for these small regions.
pixels, and estimate PEFs for these small regions. and image
and image  to get the results
to get the results  and
and  .
.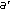 and
and 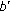 to acquire a value indicating the image differences.
to acquire a value indicating the image differences.
 " means that tha
" means that tha .DI = InfDI =
.DI = InfDI =  DI =
DI =  DI =
DI =  DI =
DI =  DI =
DI = Correct pattern
Correct pattern

