- Research Article
- Open Access
- Published:
AD-PLL for WiMAX with Digitally-Regulated TDC and Glitch Correction Logic
EURASIP Journal on Embedded Systems volume 2010, Article number: 175764 (2009)
Abstract
This paper describes the design of an All-Digital Phase Locked Loop (AD-PLL) for wireless applications in the WiMAX 3.3–3.8 GHz bandwidth. The time/digital converter (TDC) sets the in-band noise and it may be responsible for the presence of spurious tones at the PLL output. The TDC is implemented as a delay-locked loop (DLL) to be insensitive to process spreads and it uses a lead-lag phase detector and a digital loop filter to further take advantage of the digital approach. The most important source of spurs is identified in the time skew between counter and TDC in the PLL. This mechanism gives rise to a glitch in the digital feedback signal and spurs in the output spectrum. A simple glitch-corrector logic is described, that completely removes this effect, thus allowing to meet the phase noise specifications. The AD-PLL has been designed in a 90 nm CMOS process.
1. Introduction
In recent years, the mixed-signal approach not only has pervaded many applications that once were exclusively a subject for the analog design but also has begun to play an important role also in radiofrequency (RF) front-ends. As a matter of fact, the realization of software defined-radio (SDR) is one of the most important research topic in recent years [1, 2]. In these solutions, digital (or digital-like) circuits are employed not only to calibrate the circuit parameters but also to realize transceiver building blocks, often adopting a new design approach, such as transferring the information processing from the amplitude to the time domain. These techniques, besides increasing the circuit flexibility and functionality, are expected to better exploit the scaling of CMOS technology, to reduce the impact of PVT spreads, to facilitate, at least to a certain extent, the portability of a given design, and to allow for the use of automatic design tools.
The all-digital phase-locked loop (AD-PLL) represents the application of this approach to the design of PLL [3–5]. The digitization of PLL is an old idea, exploited, for instance, in the clock generators for digital circuits. In recent implementations, however, the AD-PLL is employed as frequency synthesizer for wireless systems, which implies tight specification in terms of spectral purity, that is, phase noise and spurs. This fact, for instance, still forces to use an LC-tank oscillator, to ensure the required phase noise performance. The other critical block, concerning the spectral performance, is the time-to-digital converter (TDC). This circuit is essentially the equivalent of an analog-to-digital converter, detecting time (or phase) delays. Of course, it should not rely on standard analog design solutions; otherwise some of the above mentioned advantages will be lost. The TDC is critical in many aspects: it is known that its time resolution affects the in-band noise, while the nonlinearity of its static characteristic can give rise to output spurs [4].
This work presents the design of an AD-PLL for a 3.3–3.8 GHz WiMAX transmitter. In this loop, the TDC is implemented as a digitally-regulated delay line. This is advantageous because of the simplicity of the design, but it requires some care in reducing the generated limit cycle to negligible values.
The unavoidable time skew between the TDC and the counter inputs gives rise to glitches in the AD-PLL feedback signal and ultimately to severe spurious tones in the output spectrum. This effect is not related to our specific implementation of the TDC, but it may affect any common TDC implementations. In this paper, we will show how to predict these skew-induced spurs and we will propose a digital glitch corrector, which is able to operate either when the loop is locked and when the loop is in the lock transient.
In the next Section, the operating principle of the AD-PLL including a counter and a TDC is recalled. Section 3 discusses the advantages of the closed-loop TDC, while Section 4 presents the proposed TDC and explains the presence of the limit cycle in the DLL. Section 5 discusses the generation of glitches in the presence of time skew between counter and TDC. Section 6 proposes a simple glitch-corrector logic. The schematic of the complete AD-PLL is presented in Section 7, together with the simulation results. Finally, the conclusions are drawn in Section 8.
2. Combined Operation of TDC and Counter
The basic schematic of the AD-PLL considered in this work is reported in Figure 1 [4, 6]. It is equivalent to the original structure proposed in [3], which can be obtained by simply shifting the digital integrator 
backward between the digital Frequency Control Word (FCW) and the adder, and removing the derivatives 
in the feedback path. The loop filter features a proportional-integral transfer function; its output tunes an LC-tank Digital-Controlled Oscillator (DCO) by controlling a bank of switched capacitors in parallel to the inductor. All the blocks enclosed in the gray box are clocked at the reference frequency 
.
The AD-PLL block schematic.
The error signal at the adder output 
is given by the difference between FCW and the number of DCO periods occurring within one reference period 
. The loop forces this error signal to be zero; therefore, if 
is the DCO frequency, the FCW sets the output frequency as 
. The signal 
is a digital number representing the frequency error. This number is then integrated to provide the phase error 
, whose average is forced to be zero by the loop.
With respect to the original design in [3], the open-loop gain is not altered. The advantage of the structure in Figure 1 is that the design of the adder is simpler since its input word lengths are reduced.
If the FCW were an integer number, only a counter would be necessary in the feedback path. The presence of the TDC is needed because in general FCW may have also a fractional part. For convenience, let us split FCW into two parts: an integer one (
) and a fractional one (
). The counter output provides the number of integer DCO periods within 
, that is, the integer part 
of the (
/
) ratio. The TDC quantizes the fractional part 
of (
/
). The lock conditions are 
and 
.
It is important, for what follows, to better underline the concurrent operations of the counter-TDC ensemble. The TDC input range has to cover a single reference period. We consider a very simple case in Figure 2, where FCW = 2.25 and the TDC has 8 levels or 3 bits. In a real case, the integer part of the FCW is much larger and the number of TDC bits is higher, but this simplification does not affect the present reasoning. Figure 2(a) shows that the counter output after differentiation (i.e., the number 
) is 2, for three reference clock periods out of four, and it is 3 for one clock period out of four. The TDC output after differentiation (
) provides the fractional part of the FCW, so that the frequency error 
is always zero. Note that the average value of 
is 2.25, while the average value of 
is zero. When 
increments from 2 to 3, the TDC input exceeds the limit of its dynamic; that is, it overflows, and its output after differentiation (
) becomes negative. Figure 2(b) evidences that the ensemble TDC/counter operates as a subranging ADC, which implies that the TDC characteristics must be perfectly embedded in a counter bin in the ideal case.
AD-PLL behavior for FCW = 2. 25: (a) positive edges of ref and dco, feedback signals 
and 
, and error signal 
= FCW – (
+ 
); (b) counter/TDC conversion characteristics.
At steady state, at each reference edge, the converter count will increment by 2.25 (in our example). Thus, the fractional count will increment by 0.25 and the TDC characteristic will be swept forward. It is easy to see that, in the case of 
higher than 0.5, the counter would decrease its count by one unity when the differentiated TDC output underflows and the TDC characteristic would be swept backward.
3. Closed-Loop TDC
As recalled above, the TDC is a key block for the performance of the whole AD-PLL. Figure 3 compares the basic schemes of an open- and a closed-loop TDCs. The time resolution of both of them is limited to one gate delay (i.e., about 15–20 ps in a 90 nm CMOS technology). The circuit design of the open-loop delay line is easier; however the closed-loop line, or Delay-Locked Loop (DLL), has some advantages, primarily, the independence of the time resolution over process voltage temperature (PVT) variations, since the DLL always divides the input period into 
time intervals, being the 
number of delay elements. This ensures that the quantization noise is always equal to the expected one. Conversely, in an open-loop line implemented in scaled CMOS technology, process corners may spread the delay around the nominal value up to ±50%, increasing the in-band noise uncertainty. Moreover, extra stages in the line are required to measure the whole oscillator period in the case of a fast corner.
TDC based on (a) open-loop, and (b) closed-loop delay line.
An additional advantage of the regulated delay line regards the TDC nonlinearity, which can raise the fractional spur level in ADPLLs [4]. A DLL features a better integral nonlinearity (INL) than an open-loop delay line [7], since it aligns the input and the output signal edges. Figure 4 shows the simulated INL root mean square (r.m.s.) value at each delay cell output for a 16-element delay-line both an open-loop line and a closed-loop. In the simulations, a random Gaussian delay with r.m.s.value of 5% of the nominal delay was added to each cell. The result shows that the DLL improves the INL by a factor 
in the middle of the line and by a larger factor in the second half of the line.
Simulated INL of a TDC based on an open-loop line (circles) and on a closed-loop line (triangles).
The AD-PLL presented here is intended to be used as a frequency synthesizer in a WiMAX transmitter in the 3.3–3.8 GHz band. In this application, an integral phase noise of about 
dBc is required to the synthesizer. According to Figure 2, the TDC quantizes the output phase shifts with a least significant bit (LSB) equal to 
, where τ is the time resolution of the TDC. This LSB is, in turn, related to the number 
of bits of the TDC. Thus, 
. The expression of the phase spectrum can be obtained by assuming uniform amplitude distribution and white spectrum for this quantization noise. The resulting quantization noise in the AD-PLL spectrum is 
, within the AD-PLL bandwidth. (SSCR is the Single-Sideband to Carrier Ratio.)
Setting this bandwidth to few hundreds of kHz, and the DCO phase noise to 
dBc/Hz at 1 MHz offset with 1-MHz corner frequency (between 
and 
regions), four TDC bits are sufficient to meet the integral phase noise requirements. As a consequence, the delay line needs 16 delay elements and the delay 
at 3.8 GHz should be about 
ps. This corresponds to an in-band noise plateau in the PLL spectrum of about 
dBc/Hz.
In order to meet the noise requirements, the spurious tones need to be lower than 
dBc.
4. DLL-Based TDC
The key advantage of the AD-PLL is the reduced number of analog block and of external components. Thus, the DLL-based TDC should avoid the use of analog blocks, such as charge pump and loop filter, as much as possible. In the implemented TDC, shown in Figure 5, both the phase detector (PD) and the filter are digital circuits. The PD is a set-reset flip-flop, which acts as a one-bit TDC, indicating which one of the two signals leads the other one. These circuits are sometimes referred as lead-lag or bang-bang (BB) phase detectors. The digital filter is an integrator, followed by a 6-bit current-steering DAC which regulates the bias current of the delay cells.
Schematic of the DLL-based TDC with bang-bang phase detector.
The DAC LSB sets the minimum variation of the cell delay 
(about 40 fs), which can be considered as the LSB in time domain of the regulation loop. Since the delay line features 16 stages, the delay line can cover a maximum delay variation of (40 fs) 
(16) 
(
) 
40 ps. Note that this figure in practice matches the required dynamic of the DLL, which is the difference between the period of the lowest frequency signal (3.3 GHz) and the period of the fastest signal (3.8 GHz). To add some margin for PVT variations, a coarse tuning has been realized by adding three switched capacitors of the same value at the output of each cell. This coarse control is set by the overflow/underflow of the loop integrator.
As shown in Figure 5, the PD operates at the DCO rate (3.3–3.8 GHz). At this frequency, however, the loop filter and the DAC would dissipate an excessive amount of power and the filter would require a custom design. This dissipation can be reduced by noting that no information is lost, if the filter clock is obtained by frequency-division of the DCO signal. In fact, the cell delay, and in turn the PD output, changes only after a variation of the filter output, that is, at the same rate of the digital filter clock. The only disadvantage of this choice is an increase of the DLL lock time. As reasonable trade-off has been found by dividing the input frequency by 8 and limiting the maximum clock frequency 
below (3.8 GHz)/8 = 475 MHz, this value guarantees at the same time a lock time for the maximum frequency step of about 40 ns, which is less than two reference cycles of the AD-PLL, and the possibility of using standard cells and automatic synthesis tools in the filter design [8].
The presence of the BB phase detector and the quantization of the cell delay 
which can be varied with finite resolution 
. generates a limit cycle in the DLL. A simple illustration of this behavior is sketched in Figure 6. It is necessary to know that the implemented integrator introduces, as usual, one extra clock period of latency. According to Figure 6, in t = 
the cell delay 
is below the target delay value; so, the phase detector 
changes its state and becomes one. This new value is read by the filter at the following clock rising edge and the filter output starts decreasing one clock period later at 
. Consequently, the cell delay 
starts to increase. When 
exceeds the target value (at 
), the PD toggles and the dual situation takes place. In practice, the limit cycle period is 
, where 
is the filter clock period. The peak-to-peak amplitude of the cycle at the integrator output is 3τ. This behavior is in accordance with the general results presented in [9].
The limit cycle in the DLL.
This limit cycle modulates periodically each time bin of the TDC and a spurious tone will appear at both the TDC and the AD-PLL output. Since the limit cycle at 
is sampled by the TDC flip-flops at 
, the spurious tones at the TDC output are expected to appear at 
, with integer 
. In practice, being 
, the DCO frequency 
in the 3.3–3.8-GHz range, and 
MHz, the spurious tone will fall between about 800 kHz and 11 MHz, depending on the DCO frequency.
5. Time Skew in the Counter-TDC Ensemble
The presence of a time skew between the counter and the TDC inputs is almost unavoidable. However, it causes an error in the feedback signal. Note that the phenomenon highlighted in this section is general and it does not depend on our particular TDC implementation. We consider a delay 
applied to the counter input, as shown in Figure 7. In this situation, the counter will be driven by the delayed DCO signal, indicated as dco, while the TDC input is the original DCO signal, that is, dco in Figure 7. Now, the instant in which the TDC overflows (or underflows) and that in which the counter increments (or reduces) its steady-state output does not coincide.
Time skew between the counter and TDC input signals.
To illustrate this behavior, we consider again the example discussed in Section 2. The waveforms resulting from the application of 
are sketched in Figure 8(a). Because of the skew, the counter output increments by 3 in the following reference period with respect to Figure 2. Instead, the TDC output is unperturbed. In this figure, the time skew has been assumed to be equal to 
, but the same 
and 
graphs would have been obtained for 
. The net result of the time shift of the 
sequence is the generation of a periodic bipolar glitch (with frequency 
) in the error signal 
. The average value of 
is zero; therefore the loop does not respond; however, this periodic disturbances produces spurious tones at the output. The signal 
, which is given by the accumulation of 
and is proportional to the phase error, will be a periodic square-wave with duty cycle 
.
AD-PLL behavior for FCW = 2. 25 in the presence of a time skew between counter and TDC: (a) positive edges of ref and dco, 
, 
, and 
. (b) Counter/TDC conversion characteristic.
The same impairment can be visualized by combining again the TDC and the counter conversion characteristics as shown in Figure 8(b). The effect of the positive time skew is the generation of holes in the characteristic. At steady state, this staircase is swept, going up from one step to another one. Therefore, depending on the initial phase, the converter input may periodically fall into the holes. The resulting phase error is as large as one LSB of the coarse converter, that is, of the counter.
Evaluating the fundamental frequency 
and the amplitude 
of the spur in the previous example is particularly simple. Assuming that the spur fundamental falls out of the PLL band, 
can be calculated following [10]. Thus,
with 
being the frequency response magnitude of the loop filter and 
being the DCO frequency resolution.
The example presented here is particularly simple, for the sake of clarity. In particular, the TDC has enough resolution to detect the fractional part of FCW, which makes this case similar to what happens in a standard PLL with an integer division factor. In other cases, the behavior may be slightly more complex; the main issues to be considered are listed as follows:
(i)If 
is larger than 
(in our example), the counter sequence will be shifted with respect to the TDC sequence by more than one reference cycle. So, the 
sequence will include some 0 s between +1 and –1 and its integral 
will be a sequence of pulses, whose duty cycle 
depends on the number of 0 s in the 
sequence. Thus, maximum spur amplitude in (1) occurs when 
.
(ii)We have arbitrarily assumed a phase relationship between ref and dco, given the uncertainty of the TDC quantization. Therefore, in our example, a favorable time delay between dco and ref exists which prevents to fall into the holes of the characteristic in Figure 8(b) and to generate glitches.
(iii)When 
is finer than the TDC resolution (which is the common situation), the phase relationship between ref and dco changes. Thus, the condition in (ii) may periodically occur. As a consequence, the 
and 
sequences show some missing glitches, thus slightly altering the result in (1).
6. Glitch-Correction Logic
A possible countermeasure to the glitch problem presented in the previous section has been already proposed in [11]. In that work, the derivative of 
is monitored, and if its magnitude is higher than 0.5, 
is decreased/increased by 1. In this way, the glitch in Figure 8 is removed. However, this solution has the disadvantage of altering the transient behavior. If a large variation in the DCO frequency occurs, which causes a step of +1 (or more) in the 
value, the loop would not be able to track the frequency, unless the corrector is disabled. In the case of an unexpected frequency step, that may seriously affect the lock behavior.
Instead, the circuit proposed in the present work monitors 
and 
, separately. It removes the glitch from the feedback signal and sets a flag 
, which allows to apply the 
variation simultaneously to the 
overflow/underflow. The circuit operation is shown in the flow chart in Figure 9, which is valid for 
. At the beginning, the flag 
is initialized to 0. Three main situations are taken into account.
Flow chart describing the operating principle of the glitch corrector when 
.
(a)If the integer frequency error 
differs from 0 or 1, then the loop is considered to be out of lock and no correction is applied. Thus, 
is simply given by 
and 
is not varied.
(b)In timestamp 
in the example in Figure 8(a), 
is not incremented with respect to 
, while the TDC overflows. Therefore, 
and 
. Assuming 
, the value of 
is 
, thus canceling the glitch, and 
is decremented by 1.
(c)In timestamp 
, 
is incremented with respect to 
, while the TDC does not overflow. Therefore, 
and 
. If this situation occurs after (b), the flag 
. Thus, the algorithm sets 
to 
, canceling again the glitch, and 
is incremented by 1, returning to zero.
It is easy to check that if a sudden change in the DCO frequency causes a step of +1 in 
, thanks to the adoption of the flag 
, this circuit removes only the first sample +1 of 
. Then, it leaves the loop operating normally.
The case in which 
is not reported here, for the sake of brevity. In that case, the algorithm applies a correction when 
and the TDC underflows and when 
and the TDC does not underflow. The signs of the corrections of 
and F are swapped with respect to the case in Figure 9.
7. Simulations Results
The schematic of the whole AD-PLL is sketched in Figure 10, where also the details of the loop filter are evidenced. The circuit has been designed in 90 nm CMOS technology. The digital PI loop filters features 
= 1 and 
= 16. The DCO tuning range covers the 3-4 GHz bandwidth, with 64 coarse characteristics. Each characteristic sweeps about 20 MHz with a fine tuning resolution 
= 150 kHz. The closed-loop bandwidth is about 370 kHz.
Full block schematic of the designed AD-PLL.
The AD-PLL is simulated by adding a 
phase noise to the DCO signal of 
dBc/Hz at 1 MHz offset from the carrier. The fractional FCW word is set to (95 + 1/16 + 351/
) and the reference frequency is 40 MHz. Therefore, the output frequency is 3.8025 GHz. The time skew between counter and TDC is assumed to be about 
= 15 ps, which is slightly less than one TDC LSB.
In the absence of the glitch corrector, we expect from (1) the spur fundamental to be located at 
= (1/16+351/
) 
40 MHz = 3.357 MHz and to have amplitude 
between 
and 
dBc, depending on the duty cycle 
of the 
signal. The output spectrum, simulated when the glitch corrector is disabled, is shown in Figure 11. The dominant spur is at 3.357 MHz with power of 
dBc, as predicted from theory.
Output spectrum of the AD-PLL when the glitch corrector is disabled. The dominant spur is induced by the time skew between counter and TDC.
When the glitch corrector is enabled, the skew-induced spurs disappear completely, as shown in Figure 12. The remaining dominant spur is below 
dBc, which allows to meet the phase noise requirements. This spur is caused by the DLL limit cycle, as discussed in Section 4. As expected, it falls at (
/48 
8
) 
800 kHz. The level of the in-band noise of about 
dBc/Hz is consistent with the quantization noise of the 4-bit TDC, discussed in Section 2.
Output spectrum of the AD-PLL when the glitch corrector is enabled. The dominant spur is induced by the DLL limit cycle and it is below 
dBc.
In order to highlight the neutrality of the proposed glitch corrector during the lock transient, a 10 MHz frequency step has been applied when the glitch corrector is either enabled and disabled. The output frequency (evaluated as the inverse of the output period) is shown for the two cases in Figure 13. The output frequency spikes in the absence of the corrector are caused by the +1 spikes in the 
sequence. Therefore, they are as large as 
= 2.4 MHz. Enabling the corrector allows to cancel out those spikes, without altering the lock behavior.
AD-PLL output frequency for a 10 MHz input step, when the glitch corrector is disabled (a) and enabled (b).
8. Conclusions
The design of an AD-PLL for the 3.3–3.8 WiMAX bandwidth has been presented. The main focus of this work is the design of the TDC, which sets the in-band noise performance of the synthesizer and, above all, it may be an important source of spurious tone. To fully exploit the digital-intensive approach, the TDC is implemented as a bang-bang DLL and it designed to guarantee the required time resolution. However, the unavoidable time skew between the counter and the TDC inputs in the AD-PLL is demonstrated to be responsible of generating glitches at the PLL comparison node and in turn large spurs in the PLL output spectrum. A digital glitch corrector has been presented which solves this impairment and it is able to work correctly even during a lock transient.
References
- 1.
Staszewski RB, Muhammad K, Leipold D, et al.: All-digital TX frequency synthesizer and discrete-time receiver for Bluetooth radio in 130-nm CMOS. IEEE Journal of Solid-State Circuits 2004,39(12):2278-2291.
- 2.
Abidi AA: The path to the software-defined radio receiver. IEEE Journal of Solid-State Circuits 2007,42(5):954-966.
- 3.
Staszewski RB, Wallberg JL, Rezeq S, et al.: All-digital PLL and transmitter for mobile phones. IEEE Journal of Solid-State Circuits 2005,40(12):2469-2480.
- 4.
Temporiti E, Weltin-Wu C, Baldi D, Tonietto R, Svelto F: A 3GHz fractional all-digital pLL with a 1.8 MHz bandwidth implementing spur reduction techniques. IEEE Journal of Solid-State Circuits 2009,44(3):824-834.
- 5.
Hsu C-M, Straayer MZ, Perrott MH, et al.:A low-noise wide-BW 3.6-GHz digital
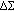fractional-N frequency synthesizer with a noise-shaping time-to-digital converter and quantization noise cancellation. IEEE Journal of Solid-State Circuits 2008,43(12):2776-2786. - 6.
Atalla E, Bashir I, Balsara P, Kiasaleh K, Staszewski RB: A practical step forward toward software-defined radio transmitters. Proceedings of the 6th IEEE Dallas Circuits and Systems Workshop on System-on-Chip (DCAS '07), November 2007, Dallas, Tex, USA 63-66.
- 7.
Henzler S, Koeppe S, Lorenz D, Kamp W, Kuenemund R, Schmitt-Landsiedel D: A local passive time interpolation concept for variation-tolerant high-resolution time-to-digital conversion. IEEE Journal of Solid-State Circuits 2008,43(7):1666-1676.
- 8.
Zanuso M, Madoglio P, Levantino S, Samori C, Lacaita A: Time-to-digital converter for frequency synthesis based on a digital bang-bang. to appear in IEEE Transactions on Circuits and Systems I
- 9.
Da Dalt N: A design-oriented study of the nonlinear dynamics of digital bang-bang PLLs. IEEE Transactions on Circuits and Systems I 2005,52(1):21-31.
- 10.
Lacaita A, Levantino S, Samori C: Integrated Frequency Synthesizers for Wireless Systems. Cambridge University Press, Cambridge, UK; 2007.
- 11.
Lee M, Heidari ME, Abidi AA: A low noise, wideband digital phase-locked loop based on a new time-to-digital converter with subpicosecond resolution. Proceedings of IEEE Symposium on VLSI Circuits, June 2008, Honolulu, Hawaii, USA 104-105.
fractional-N frequency synthesizer with a noise-shaping time-to-digital converter and quantization noise cancellation. IEEE Journal of Solid-State Circuits 2008,43(12):2776-2786.Acknowledgment
This work was partially supported by the Communication Integration Research Lab of Intel Corp., Hillsboro OR.
Author information
Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Levantino, S., Zanuso, M., Madoglio, P. et al. AD-PLL for WiMAX with Digitally-Regulated TDC and Glitch Correction Logic. J Embedded Systems 2010, 175764 (2009). https://doi.org/10.1155/2010/175764
Received:
Accepted:
Published:
Keywords
- Phase Noise
- Clock Period
- Loop Filter
- Cell Delay
- Spurious Tone
